A Comprehensive Guide to Graph Search in Python - Part 2, Breadth-First Search

Breadth-First Search (BFS)

Unlike DFS, which goes deep in a certain direction first before considering another direction, BFS will analyze the next node in each possible direction first and then repeat the process for the next node in each direction. So instead of working on one path/direction all the way, it is analyzing all the possible paths at the same time, node to node. It will analyze the first node in each direction, and then analyze the second node each direction, and repeat the process until the target node is found. Once the target node or solution is found, it stops looking.

Pros and Cons:

This algorithm is guaranteed to find the optimum solution as it will be going over all the paths at the same time and which ever reaches the goal first will be the optimum path/solution. However, it is almost guaranteed to take longer and it can be the longest way to reach the goal. Imagine the goal node is the last node on the last path, it will have to analyze each and every node before it reaches the goal node. Similarly, the bigger the graph, the slower the algorithm can be potentially since it has to process the nodes in every possible direction.

At the same time, the algorithm is guaranteed to find the optimum solution or the shortest path. So if finding the shortest path is the goal and time is not a priority, this algorithm may be the one.

Coding BFS:

Consider the following graph:

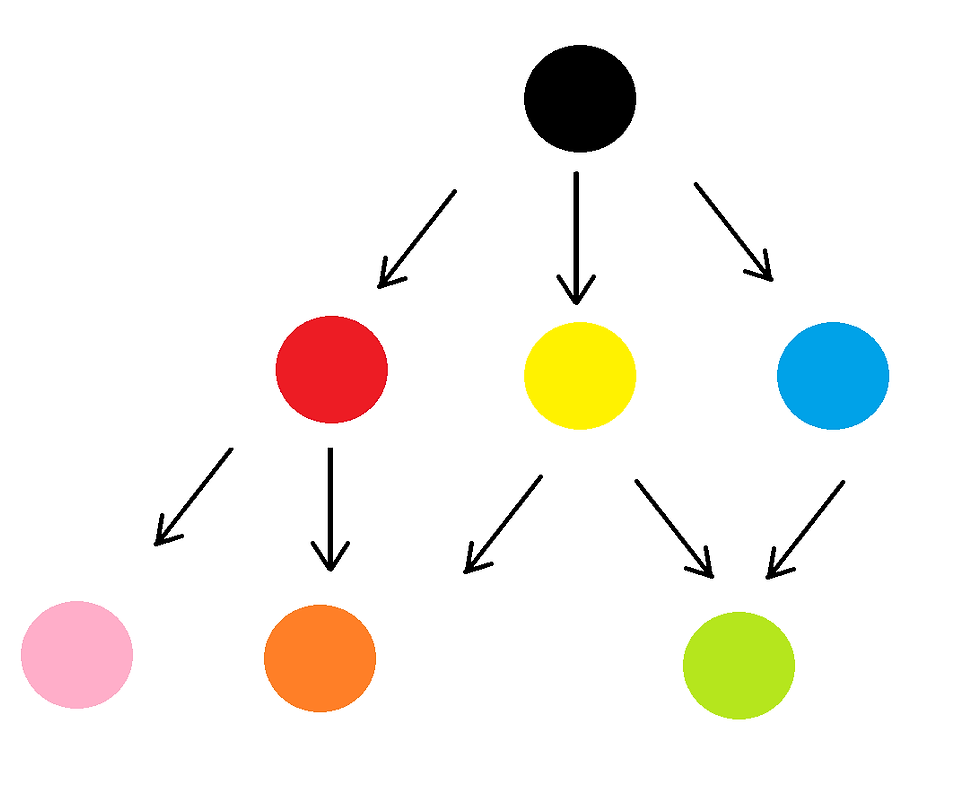
We can represent it programmatically as following:

graph = {
'Black':['Red', 'Yellow', 'Blue'],
'Red':['Pink', 'Orange'],
'Yellow':['Orange', 'Green'],
'Blue':['Green'],
'Pink':[],
'Orange':['Green'],
'Green':[]
}

Now let’s write our BFS function, which takes the the graph as well as the starting node as input and prints out the nodes as it processes them. Since BFS checks our a node in every direction, it will go through our graph layer by layer while keeping track of every node it has processed by adding it to a queue.

def bfs(graph, root):visited, queue = set(), collections.deque([root])
    visited.add(root)while queue:# Dequeue a vertex from queue
        vertex = queue.popleft()
        print(str(vertex) + " ", end="")# If not visited, mark it as visited, and
        # enqueue it
        for neighbour in graph[vertex]:
            if neighbour not in visited:
                visited.add(neighbour)
                queue.append(neighbour)

Now we call our function with ‘Black’ as the starting node.

bfs(graph, ‘Black’)

We will get an output like this:

Black Red Yellow Blue Pink Orange Green

As we can see, it went through each node layer by layer, unlike DFS which would have gone in one specific direction first rather than going layer by layer.

Applications of BFS:

BFS has many applications. Common ones are peer to peer networks like BitTorrent where BFS is used to find all neighbor nodes. Web crawlers and search engines also use BFS by starting from a source page and then follow all links from there. DFS can also be used by crawlers however considering how vast the world wide web is, the algorithm probably would not go beyond one branch. Neighboring locations in navigation are also found using BFS. An interesting use is in garbage collection sing Cheney’s algorithm.

References:

1. Breadth-First Search

2. Applications of Breadth First Adversarial